Core Research
Executive Summary
Option Research and Technology Services (ORATS), established in 2001, provides US equity options data designed by successful options traders. ORATS proprietary data including implied summarizations and historical volatility readings, have been shown in backtesting to be important predictors of profitable trading strategies. Component weighted averages, forward and flat volatilities, contango, and constant maturity implied volatilities at various deltas set ORATS data apart.
Volatility Research
Our proprietary historical volatilities are calculated from intraday data market information and produce more accurate daily volatilities than traditional methods like close-to-close. From these accurate volatilities, we produce effective forecasts of volatility and other useful datasets.
The ORATS implied volatility summarization technique produces an accurate smoothed market value curve. This single line fits between the calls and puts bid-ask at a high rate. These volatilities create high-quality options Greeks like delta, vega, gamma, and theta. These data points are especially useful in backtesting where accuracy is important. Our method of summarizing the implied volatility surface allows simplification of strike relationships to a few factors. These factors are comparable over time and across related equities and produce an effective forecasted volatility surface.
Asset Coverage
ORATS covers all US equity options including stocks, ETFs, and indexes--over 4000 tickers. Also included are component weighted averages for the major indexes and ETFs, over 30 more tickers delineated with an underscore C added to the ticker, i.e. NDX_C and IWM_C. These component tickers provide difficult to come by historical weighed averages each data set in Exhibit A and Exhibit B. Here is a list of the indexes and ETFs:
ALL_C, DIA_C, DJX_C, GDX_C, IBB_C, IGN_C, ITB_C, IWM_C, IYR_C, KBE_C, KRE_C, MDY_C, NDX_C, NQX_C, OIH_C, QQQ_C, RUT_C, SMH_C, SPX_C, SPY_C, XBI_C, XHB_C, XLB_C, XLC_C, XLE_C, XLF_C, XLI_C, XLK_C, XLP_C, XLRE_C, XLU_C, XLV_C, XLY_C, XOP_C, XSP_C
Historical Volatility Research
In addition to offering traditional close-to-close realized volatility computations, we offer a second way to view historical volatility. Our proprietary historical volatilities are calculated from intraday open-high-low-close stock price market information and produce more accurate daily volatilities than traditional methods like close-to-close.
Related Data Point(s): orHv1d, orHv5d, clsHv5d
Ex-Earnings Historical Volatility
Close-to-close and ORATS historical volatilities are also presented with the day of and day after earnings taken out of the calculation. These calculations are important as they can be compared over time or when analyzing a non-earnings expiration.
Related Data Point(s): orHvXern5d, clsHvXern5d
Implied Volatility
The ORATS implied volatility summarization technique produces an accurate smoothed market value curve. This single line fits between the calls and puts bid-ask at a high rate. Our method of summarizing the implied volatility surface allows simplification of strike relationships to a few factors, at-the-money implied volatility readings, constant maturity readings ie 30 days, slope of the strike implied volatility skew and curvature of that skew. These factors are comparable over time and across related equities and produce an effective forecasted volatility surface.
ORATS presents the implied volatility and forecasts for the first four months with standard expirations on the third Friday of the month. Seeing all standard options expirations allows for assessment of the implied volatility across assets and against monthly forecasts.
Related Data Point(s): atmIvM1, atmIvM2
Interpolated Implied Volatility
The constant maturity implied volatility is calculated by measuring the two expirations around the day to be measured. ORATS presents the 30, 60, 90 days, 6 months and 1 year interpolated implied volatility.
Related Data Point(s): iv20d, iv30d
Interpolated Implied Volatilities At Various Deltas
ORATS presents the constant maturity implied volatilities at various delta levels in addition to at-the-money 50 delta: The 5, 25, 75 and 95 call delta IVs are also presented.
Related Data Point(s): vol5, vol25, vol50
Constant Maturity Ex-Earnings Implied Volatility and Earnings Effects
The most important measurements are constant maturity implied volatilities, and especially with earnings effects taken out of the implied volatility. As a result of our accurate implied volatilities and sophisticated methods of term structure modeling, ORATS determines the additionally implied volatilities in the expiration months that are affected by earnings announcements, what we call the Implied Earnings Move. Implied earnings moves are taken out of the implied volatility term structure by solving for the resulting ex-earnings implied skew versus a rational implied volatility term structure model.
Related Data Point(s): orIvXern20d, orIvXernInf
Earnings Moves Studies
The Implied Earnings Moves can be compared to the average absolute actual earnings moves in a stock. This simple earn move calculation is the absolute value of the last twelve percentage moves in the stock after an earnings announcement.
Related Data Points(s): ernMv1, ernMv2, impErnMv
Implied Earnings Effects vs. Forecasted Earnings Effects
Once we defined a smooth surface across time to expiration and delta, we were then ready to utilize the earnings event studies of historical volatility to produce Forecasted Earnings Effects. As a result of our research, we utilize actual stock moves on earnings announcement dates to make a forecast of future moves. As a result of our accurate implied volatilities and sophisticated methods of term structure modeling, ORATS determines the additionally implied volatilities in the expiration months that are affected by earnings announcements, what we call the Implied Earnings Effects. The months that are affected by earnings announcements are those that have an expiration date after the upcoming expected earnings announcement date. With a forecast earnings announcement effect and simple variance math, we can make the correct adjustments to the implied volatility surface. In most cases, the implied volatility is increased in the months that are affected by earnings announcements since most equities are more volatile on the days surrounding an earnings announcement than would otherwise be expected. Twelve historical earnings effects are presented.
Related Data Point(s): impliedEe, impErnMv
Earnings Event Studies
One of the other uses for this accurate volatility measure is studying a predictable event’s effect. One study we perform measures the effect of periodic earnings announcements on volatility. Once the effect is measured, it can be forecast and thus, priced into the theoretical values for the expiration months it affects. This simple earn move calculation is the percentage move. The earnings effect calculation assesses the move of the stock price on announcement day regarding the percentage of market expectation of a normal move on a day without earnings.
Related Data Point(s): ernEffct1, ernMv1, absAvgErnMv
Implied Volatility Surface
ORATS describes the implied volatility surface as a 3-dimensional surface where the independent variables are time to expiration, and option delta and the dependent variable is implied volatility. To illustrate an implied volatility surface, we have developed a 2-dimensional graph that displays all three axes in the figure below. Summary information about this surface gives the trader a macro view of the implied volatilities for each option chain. ORATS takes a snapshot of all options on all symbols approximately 14 minutes before the close of trading. Options markets from this time are often of higher quality than at the close.
ORATS measures the surface using the following summary characteristics: at-the-money volatility, strike slope, and derivative (curvature).
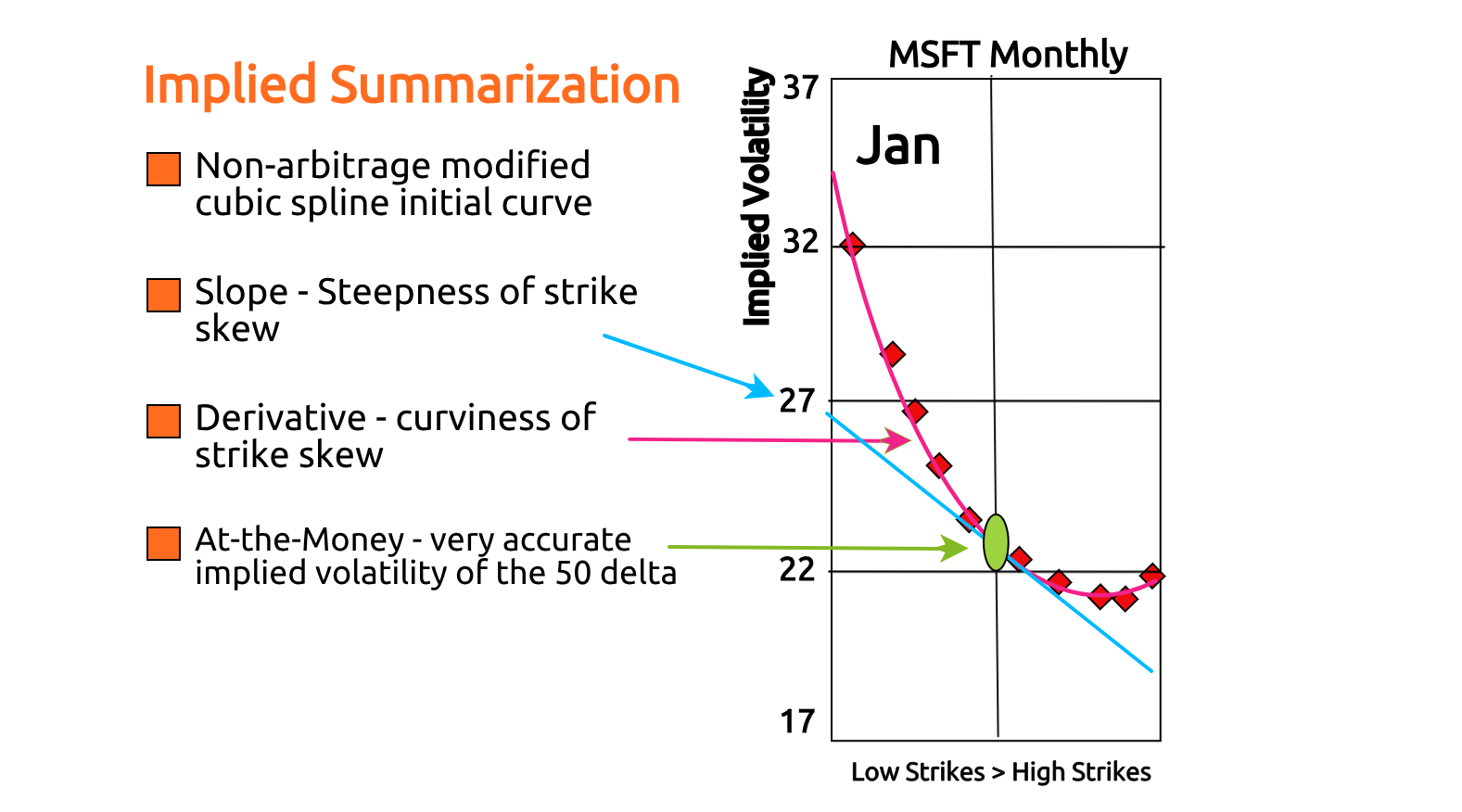
The "Smile"
At-the-money volatility is the implied volatility at the 50 delta call and put. Strike Slope is a measure of the amount that implied volatility changes for every increase of 10 call delta points within the intra-month skew. It measures how lopsided the 'smile' or 'smirk' is. The derivative is a measure of the rate at which the strike slope changes for every increase of 10 call delta points within the intra-month skew. It measures the curvature of the intra-month skew or 'smile.' We chose just two parameters to describe the skew to get a reasonable fit for the fewest assumptions.
Using this method of describing the skew has the additional benefit of producing accurate at-the-money volatility readings important for summarizing the term structure.
Related Data Point(s): slope, slopeInf, deriv, derivInf
Forecasting the Implied Volatility Surface
These sophisticated methods of summarizing and manipulating the implied volatility surface allow us to compare summary characteristics across related equities and over time. These observations are then used in volatility forecasting models. In options trading, to find an edge, it is useful to compare implied volatility surface parameters and market values to forecasted parameters and to theoretical values computed using these parameters.
Related Data Point(s): orFcst20d, orIvFcst20d, orFcstInf, slopeFcst, slopeFcstInf, derivFcst, derivFcstInf, fcstR2, fcstR2Imp, impliedR2
Advanced: Calculating an Implied Volatility for Each Strike
Given the at-the-money implied volatility, the slope and the derivative, an implied volatility can be calculated for each strike. First, a call delta is calculated for the strike using a standard option pricing model (not provided). Second, the slope and derivative for the expiration is calculated given the interpolated slope and derivative for that expiration. Third, the implied volatility formula is used to determine the strike implied.
Formula: Atmiv*(1+(slope/1000+(deriv/1000*(delta100-50)/2))(delta*100-50))
For example, assume the following:
| Field | Value |
|---|---|
| atmIvM1 | 30 |
| slope | 1 |
| deriv | 0.1 |
| delta | 0.75 |
| dte | 30 |
Since we are finding the month 1 volatility the 30 day slope and derivative can be used:
30*(1+(1/1000+(0.1/1000*(0.75100-50)/2))(0.75*100-50)) = 31.688
Example 2, assume:
| Field | Value |
|---|---|
| 30dayatmiv | 32 |
| infiniteATMIV | 28 |
| slope | 1 |
| deriv | 0.08 |
| slopeInf | 2 |
| derivInf | 0.1 |
| delta | 0.25 |
| dte | 90 |
In this example we first need to interpolate the IV, slope and derivative between the 30 day and in the infinite. This is done by weighting the 30day * 81% and the infinite 19% (see below).
IV = 0.81 _ 32 + 0.19 _ 28 = 31.26 Slope = 0.81 _ 1 + 0.19 _ 2 = 1.19 Derivative = 0.81 _ 0.1 + 0.19 _ 0.08 = 0.084 Implied volatility at 25 delta: 31.26*(1+(1.19/1000+(0.084/1000*(0.25100-50)/2))(0.25*100-50))=31.15
NEW - Finding the interpolation weightings between the 30 day and in the infinite: The weightings are found by first calculating the target days difference between the 30 day and 2 year (used for infinite days to expiration). For DTE < 30 us the 30 day reading. For DTE> 730 (2*365) us the infinite reading alone. For those DTE between 30 and 730 use the following method:
- Calculate the square roots for 30 days, 730 days and the target date, here 90 days.
- Total the absolute difference between square roots of the target DTE and 30 and 730.
- The weighting for each is the complement of the difference divided by the total error.
| DTE | Sqrt | Errors | Weight | |
|---|---|---|---|---|
| Target | 90 | 9.49 | ||
| 30 DTE | 30 | 5.48 | 4.01 | 0.81 |
| Infinite | 720 | 27.02 | 17.53 | 0.19 |
| Total Errors | 21.54 |
In the example of finding the weights for 90 DTE:
- The square root of 90 is 9.49, of 30 is 5.48 and of 730 is 27.02.
- The total errors is (9.49-5.48)=4.01 plus (27.02-9.49)=17.53 total is 21.54.
- The complement for the 30 day is 17.53/21.54=.81 and the infinite is .19
Thus to find a weighted 30 day and in the infinite, multiply each reading by the above ratios.
Assessing the First Earnings Month’s IV
The first expiration after the earnings announcement is the most important for earnings traders. ORATS identifies the implied volatility of the first expiration and compares this to the following two IVs to assess under or overvalued.
- Ex-earnings implied volatility of the first expiration after earnings plus the implied earnings effect and
- The term structure of ATM IV are simultaneously solved with a short term and long term points, earnings effect added to months after earnings announcements, and a 45-day additional adjustment.
After the term solve, the additional earnings effect on the months after earnings announcement are displayed.
Related Data Point(s): fairVol90d, fairXieeVol90d, fairMth2XieeVol90d, impErnMv90d, impErnMvMth290d
The Rip Value
When on the floor Matt Amberson noticed experienced traders paying more than theoretical value for certain low priced options. Also, these traders would not hedge all the theoretical deltas from these options. The options seemed to have a low price but would vary between stocks. I set out to define what this level was and the result was the Rip Value. The Rip Value is the value where traders would start to pay more for options and also start to take deltas out of their positions. ORATS uses the Rip for these two methods and also as a trigger to exit options in the backtesting platform. The specific formula and implementation techniques can be had by contacting matt@orats.com.
Related Data Point(s): rip
Correlation to SPY and ETF
ORATS presents the correlation to the SPY and the related ETF for one month and one year.
Related Data Point(s): correlSpy1m, correlSpy1y, correlEtf1m, correlEtf1y
Beta to SPY
ORATS presents the traditional beta calculation of the stock to the SPY for one year.
Related Data Point(s): beta1m, beta1y
Percentile Analysis
It is useful to see where the current reading of a variable is in relation to a time series of observations. The percentile takes all the observations, sorts them, and makes an assessment of where the current reading is on that list. To calculate percentile, you sort the list of numbers. Then you find the number in question from the list and take that index and divided by the length of the list. So an example of getting the current percentile of IV = 15 from the list of [8,15,12,10,6,20,25,30]. Sort the list [6,8,10,12,15,20,25,30]. Find the index number IV= 15 in the list, which is 5th index. The percentile = 5 / 8 = 62.5%
Related Data Point(s): ivPctile1m, ivPctile1y, ivPctileSpy, ivPctileEtf
IV Ratios to SPY and ETF
It is useful to monitor the ratio of the stock implied volatility to the SPY and related ETF. ORATS presents the ratio and the average of the ratio over time and the standard deviation of the ratio.
Related Data Point(s): ivSpyRatio, ivSpyRatioAvg1m, ivSpyRatioAvg1y, ivSpyRatioStdv1y, ivEtfRatio, ivEtfRatioAvg1m, ivEtfRatioAvg1y, ivEtFratioStdv1y
IV HV Ratios
Another important indicator is how the implied volatility is trading in relation to the historical volatility. It is useful to compare that ratio to the related ETF ratio to see if the ratio is high or low.
Related Data Point(s): ivHvXernRatio, ivHvXernRatio1m, ivHvXernRatio1y, ivHvXernRatioStdv1y, etfIvHvXernRatio, etfIvHvXernRatio1m, etfIvHvXernRatio1y, etfIvHvXernRatioStdv1y
Residual Measurements from Put Call Parity
ORATS measurements of implied volatility include equating the call and put implied volatilities by solving for residual yield. Options pricing formulas use a risk-free yield and a dividend yield to produce a theoretical option value. ORATS holds the other inputs in the pricing formula and solves for the residual yield, the remaining yield after interest and dividends. Deconstructing residual yield produces approximations of the implied dividends and the implied borrow rate in market options prices.
Related Data Point(s): impliedNextDiv, annActDiv, annIdiv, error, confidence
Borrow Rate
This observation is calculated by averaging the following calculation performed for each strike that is traded for a specific underlying asset: Average of the call market bid ask prices minus the call theoretical value plus the average of the put market bid ask prices minus the put theoretical value. Theoretical values are computed using the following inputs: publicly announced inputs for interest and dividends; and volatility based on the implied volatility of the average of the market bid ask prices. Higher values for Borrow indicate that the option prices are implying that any or all of the following inputs are different than what is expected: interest, dividends, and hedge price.
Related Data Point(s): borrow30, borrow2yr
Earnings Announcement Historical Dates and Moves
ORATS presents the past 12 earnings dates and earnings information.
Related Data Point(s): ernDate1, ernDate2, ernDate3, ernDate12
Current Straddle Pricing
ORATS presents the current straddle pricing from the at-the-money options along with the strike used in pricing, and the theoretical prices from smoothed and forecasted volatility surfaces. As earnings announcement date nears, the current prices can be compared to historical dates the day before earnings.
Related Data Point(s): ernStraPct1, straPxM1, smoothStraPxM1, fcstStraPxM1, loStrikeM1
Forward Implied Volatility
The forward volatility is a measure of the implied volatility over a period in the future extracted from IV at the beginning of that period and the end of that period. ORATS calculates forwards using the neighboring constant maturity implied volatilities 20, 30, 60, 90 and 180 days and the 30 to 90 day period.
Related Data Point(s): fwd30_20, fwd60_30
Flat Forward Implied Volatility
The flat forward volatility is a measure of the implied volatility over a period in the future using theoretical pricing relationships from IV at the beginning of that period and the end of that period. ORATS calculates flat forwards using the neighboring constant maturity implied volatilities 20, 30, 60, 90 and 180 days and the 30 to 90 day period.
Related Data Point(s): ffwd30_20, ffwd60_30
Flat Forward Divided by Forward Implied Volatility
The flat forward volatility divided by the forward volatility can produce meaningful signals on future volatility behavior of the underlying instrument based on IV levels of the term structure. ORATS calculates flat forwards divided by forwards using on the neighboring constant maturity implied volatilities 20, 30, 60, 90 and 180 days and the 30 to 90 day period.
Related Data Point(s): fbfwd30_20, fbfwd60_30
Ex-Earnings Forward Implied Volatility
The forward volatility is a measure of the implied ex-earnings volatility over a period in the future extracted from IV at the beginning of that period and the end of that period. ORATS calculates forwards using the neighboring constant maturity implied ex-earnings volatilities 20, 30, 60, 90 and 180 days and the 30 to 90 day period.
Related Data Point(s): fexErn30_20, fexErn60_30
Ex-Earnings Flat Forward Implied Volatility
The flat forward ex-earnings volatility is a measure of the implied ex-earnings volatility over a period in the future using theoretical pricing relationships from IV at the beginning of that period and the end of that period. ORATS calculates flat forwards using the neighboring constant maturity implied ex-earnings volatilities 20, 30, 60, 90 and 180 days and the 30 to 90 day period.
Related Data Point(s): ffexErn30_20-20, ffexErn60_30
Ex-Earnings Flat Forward Divided by Forward Implied Volatility
The flat forward ex-earnings volatility divided by the forward ex-earnings volatility can produce meaningful signals on future ex-earnings volatility behavior of the underlying instrument based on IV levels of the term structure. ORATS calculates flat forwards divided by forwards using on the neighboring constant maturity implied ex-earnings volatilities 20, 30, 60, 90 and 180 days and the 30 to 90 day period.
Related Data Point(s): fbfexErn30_20, fbfexErn60_30
Other Research
It is often useful to eliminate potential and actual takeover targets from scanning and research. ORATS has methods for identifying potential targets and makes assessments whether it would serve our customers to include these stocks in the list. When identifying stocks on which to trade options, it is often important to consider liquidity. ORATS calculates the average option volume over the last 20 days.
Related Data Point(s): avgOptVolu20d, tkOver
