Indicators
Thursday, May 23rd 2019
Modeling the Implied Volatility Surface: Skewness and Kurtosis
Here's the ORATS approach to skewness and kurtosis, what we call slope and derivative for strike skew parameters.
Summary
ORATS uses slope and derivative to describe the implied volatility surface, which can be calibrated using term structure and earnings effect. This approach produces accurate at-the-money volatility readings, allows for comparison to other stocks and periods, and enables forecasting and computing of a reasonable volatility surface and good greeks. The Data API provides access to historical and current slope and derivatives. An implied volatility can be calculated for each strike given the at-the-money implied volatility, slope, and derivative using a formula. The interpolation weightings between the 30 day and infinite are found by calculating the target days difference between them.
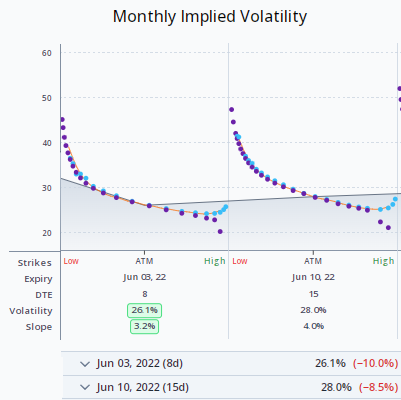
To break down the implied volatility surface at ORATS, we look at the term structure in three points: 30 day IV, 2 year IV, and earnings effect. We summarize the strike relationships in two points, slope and derivative. From those five points, most of the surface can be calibrated. There still needs to be work done on the wings, which is a separate issue.
We looked at term structure in a separate blog: Implied Volatility Term Structure and Interpolated IVs so in this blog we will look at slope and derivative, which some call skewness and kurtosis.
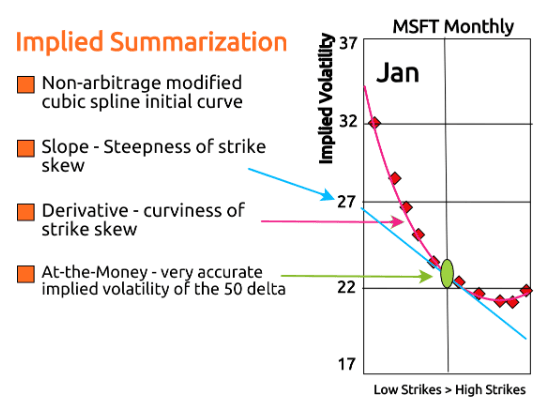
An implied volatility surface for a month can be described as a 2-dimensional surface where the independent variables option delta and the dependent variable is implied volatility. ORATS solves for the surface using the following summary characteristics, strike slope and derivative.
Strike Slope is a measure of the amount that implied volatility changes for every increase of 10 call delta points within the intra-month skew. It measures how lopsided the 'smile' or 'smirk' is. The derivative is a measure of the rate at which the strike slope changes for every increase of 10 call delta points within the intra-month skew. It measures the curvature of the intra-month skew or 'smile.' We chose just two parameters to describe the skew to get a reasonable fit for the fewest assumptions.
Using this method of describing the skew has the additional benefit of producing accurate at-the-money volatility readings important for summarizing the term structure.
Another benefit of this approach is the ability to:
- Compare the slope and deriviative readings to other stocks and to other historical periods, even when the stock price or implied volatility level was much different.
- Forecast the parameters of the skew and make some assessment of under or over valued.
- Compute a reasonable volatility surface and produce good greeks.
- Compare individual stock readings to related ETFs or indexes to get a relative value of slope and derivative.
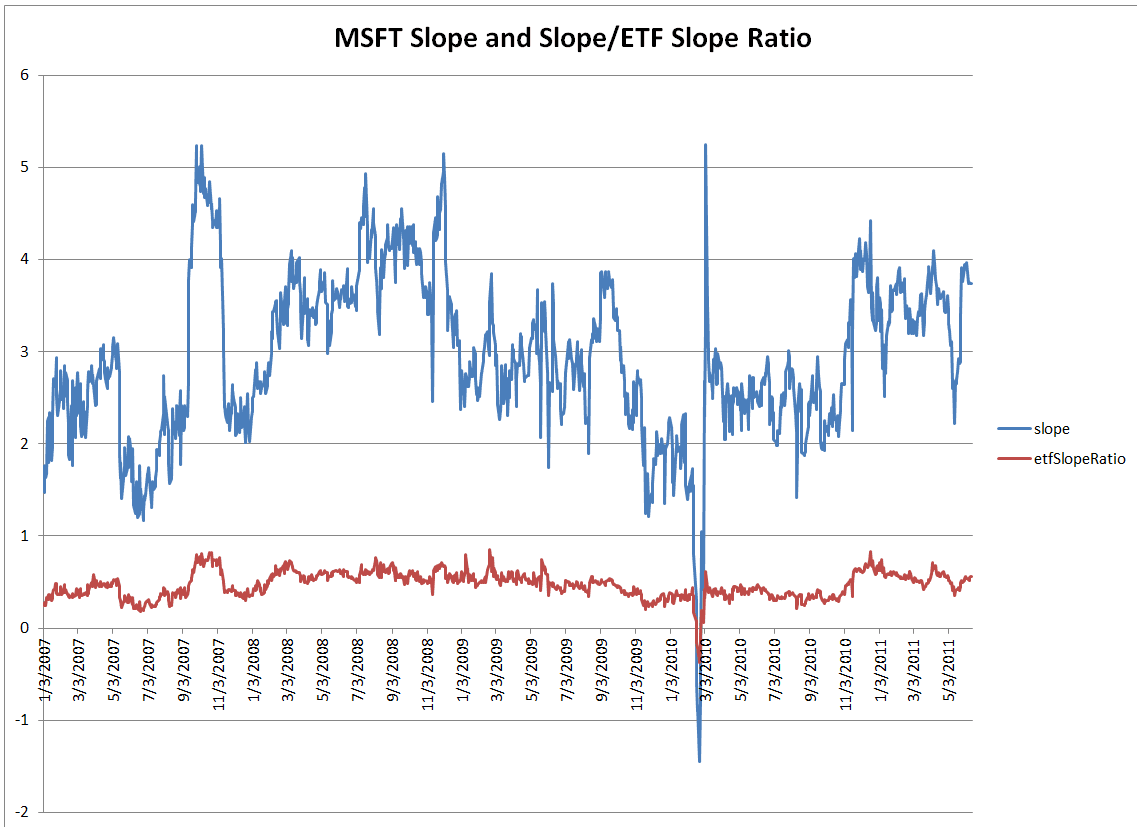
The Data API has access to a trove of historical and current slope and derivatives based on delayed market quotes. Here's a graph of MSFT slope in Blue and MSFT slope divided by the XLK (MSFT's best ETF) in Red. That valley around 2/22/10 was when MSFT stock price went from mid $80s to mid $90s.
Given the at-the-money implied volatility, the slope and the derivative, an implied volatility can be calculated for each strike. First, a call delta is calculated for the strike using a standard option pricing model (not provided). Second, the slope and derivative for the expiration is calculated given the interpolated slope and derivative for that expiration. Third, the implied volatility formula is used to determine the strike implied.
Formula: Atmiv*(1+(slope/1000+(deriv/1000*(delta*100-50)/2))*(delta*100-50))
For example, assume the following:
Since we are finding the month 1 volatility the 30 day slope and derivative can be used. 30*(1+(1/1000+(0.1/1000*(0.75*100-50)/2))*(0.75*100-50)) = 31.688
Example2, assume:
In this example we first need to interpolate the IV, slope and derivative between the 30 day and in the infinite. This is done by weighting the 30day * 81% and the infinite 19% (see below).
IV = 0.81 * 32 + 0.19 * 28 = 31.26 Slope = 0.81 * 1 + 0.19 * 2 = 1.19 Derivative = 0.81 * 0.1 + 0.19 * 0.08 = 0.084 Implied volatility at 25 delta: 31.26*(1+(1.19/1000+(0.084/1000*(0.25*100-50)/2))*(0.25*100-50))=31.15
NEW - Finding the interpolation weightings between the 30 day and in the infinite: The weightings are found by first calculating the target days difference between the 30 day and 2 year (used for infinite days to expiration). For DTE < 30 us the 30 day reading. For DTE> 730 (2*365) us the infinite reading alone. For those DTE between 30 and 730 use the following method:
- Calculate the square roots for 30 days, 730 days and the target date, here 90 days.
- Total the absolute difference between square roots of the target DTE and 30 and 730.
- The weighting for each is the complement of the difference divided by the total error.
In the example of finding the weights for 90 DTE:
- The square root of 90 is 9.49, of 30 is 5.48 and of 730 is 27.02.
- The total errors is (9.49-5.48)=4.01 plus (27.02-9.49)=17.53 total is 21.54.
- The complement for the 30 day is 17.53/21.54=.81 and the infinite is .19
Thus to find a weighted 30 day and in the infinite, multiply each reading by the above ratios.
More reading:
Disclaimer:
The opinions and ideas presented herein are for informational and educational purposes only and should not be construed to represent trading or investment advice tailored to your investment objectives. You should not rely solely on any content herein and we strongly encourage you to discuss any trades or investments with your broker or investment adviser, prior to execution. None of the information contained herein constitutes a recommendation that any particular security, portfolio, transaction, or investment strategy is suitable for any specific person. Option trading and investing involves risk and is not suitable for all investors.
All opinions are based upon information and systems considered reliable, but we do not warrant the completeness or accuracy, and such information should not be relied upon as such. We are under no obligation to update or correct any information herein. All statements and opinions are subject to change without notice.
Past performance is not indicative of future results. We do not, will not and cannot guarantee any specific outcome or profit. All traders and investors must be aware of the real risk of loss in following any strategy or investment discussed herein.
Owners, employees, directors, shareholders, officers, agents or representatives of ORATS may have interests or positions in securities of any company profiled herein. Specifically, such individuals or entities may buy or sell positions, and may or may not follow the information provided herein. Some or all of the positions may have been acquired prior to the publication of such information, and such positions may increase or decrease at any time. Any opinions expressed and/or information are statements of judgment as of the date of publication only.
Day trading, short term trading, options trading, and futures trading are extremely risky undertakings. They generally are not appropriate for someone with limited capital, little or no trading experience, and/ or a low tolerance for risk. Never execute a trade unless you can afford to and are prepared to lose your entire investment. In addition, certain trades may result in a loss greater than your entire investment. Always perform your own due diligence and, as appropriate, make informed decisions with the help of a licensed financial professional.
Commissions, fees and other costs associated with investing or trading may vary from broker to broker. All investors and traders are advised to speak with their stock broker or investment adviser about these costs. Be aware that certain trades that may be profitable for some may not be profitable for others, after taking into account these costs. In certain markets, investors and traders may not always be able to buy or sell a position at the price discussed, and consequently not be able to take advantage of certain trades discussed herein.
Be sure to read the OCCs Characteristics and Risks of Standardized Options to learn more about options trading.
Related Posts