Indicators
Monday, April 18th 2022
Options 101: Estimating Options Future Values Given Change In Stock Price
Estimate the price of an option given the change in the underlying price using options greeks, delta and gamma. Also, using a change in the distribution can show the future price.
Summary
This article explains how to estimate the future value of an option given a change in the underlying price using options greeks, delta and gamma. It also suggests adjusting the future distribution to show the future price if your prediction is not precise. The article provides an example of using delta and gamma to estimate the future value of a SPY $440 call with 30 days to expiration and a stock price of $437.92, resulting in an ending price of $22.14. Shifting the future distribution based on a 5% increase in the underlying price results in a value of $22.99, which is close to the delta and gamma estimate.
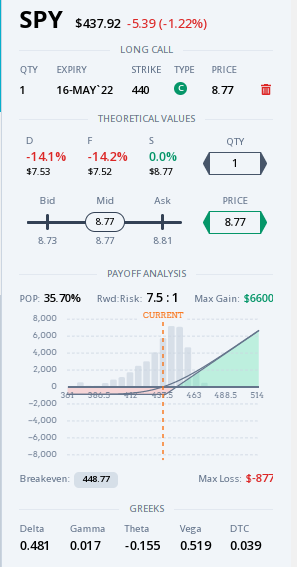
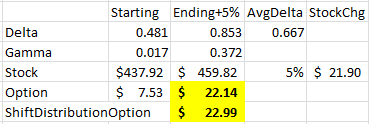
If you want to know what the price of an option will be based on the change in the underlying price, you can use the greeks to get an estimate. For example, if SPY goes up 5%, what will be the future value of a SPY $440 call with 30 days to expiration, SPYprice $437.92 a delta of 0.481 and a gamma of 0.017?
Delta is the change in the price of the option given a change in the underlying price.
Gamma is the change in delta given a change in the underlying price.
Start by getting a good average delta for the entire move in the underlying. You can average the starting delta with the ending delta to get this estimate. We know the starting delta. The ending delta is the gamma * underlyingChange + delta.
Ending delta = 0.481 + gammaEffect 0.372 = 0.853
Average delta = (0.481 + endingDelta 0.853) = 0.667
deltaEffect = stockChange $21.90 * avgDelta 0.667 = 14.61
Ending price of call = startingPrice $7.53 + deltaEffect $14.61 = $22.14
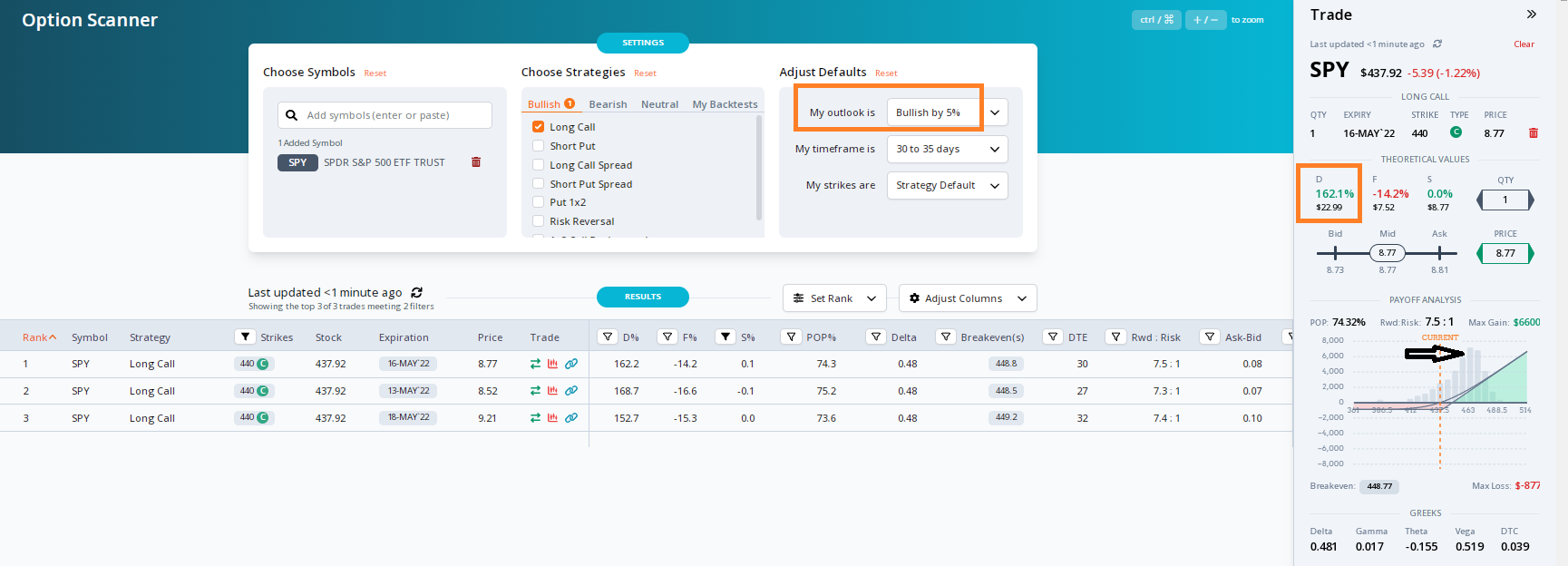
Another way to think about changes in options prices when your prediction is not precise is adjusting the future distribution. If you construct a distribution of future returns based on the time to options expiration that has a zero expected value for the stock, ie summing the percents * stock moves = 0, you can shift the future expectation to whatever your outlook is.For example, if you think SPY will be up 5% in 30 days, the current distribution D% values the 16-May $440 call at $7.53. Up 5% values it at $22.99.You can compare the traditional approach to using delta and gamma to forecast a change in options prices to shifting the distribution. The result is close $22.14 vs D% of $22.99.
In summary:
$22.14 = avgDelta .667 * stockChg 21.90 + origOption 7.53avgDelta .667 = gamma 0.017 * stockChg 21.9
Disclaimer:
The opinions and ideas presented herein are for informational and educational purposes only and should not be construed to represent trading or investment advice tailored to your investment objectives. You should not rely solely on any content herein and we strongly encourage you to discuss any trades or investments with your broker or investment adviser, prior to execution. None of the information contained herein constitutes a recommendation that any particular security, portfolio, transaction, or investment strategy is suitable for any specific person. Option trading and investing involves risk and is not suitable for all investors.
All opinions are based upon information and systems considered reliable, but we do not warrant the completeness or accuracy, and such information should not be relied upon as such. We are under no obligation to update or correct any information herein. All statements and opinions are subject to change without notice.
Past performance is not indicative of future results. We do not, will not and cannot guarantee any specific outcome or profit. All traders and investors must be aware of the real risk of loss in following any strategy or investment discussed herein.
Owners, employees, directors, shareholders, officers, agents or representatives of ORATS may have interests or positions in securities of any company profiled herein. Specifically, such individuals or entities may buy or sell positions, and may or may not follow the information provided herein. Some or all of the positions may have been acquired prior to the publication of such information, and such positions may increase or decrease at any time. Any opinions expressed and/or information are statements of judgment as of the date of publication only.
Day trading, short term trading, options trading, and futures trading are extremely risky undertakings. They generally are not appropriate for someone with limited capital, little or no trading experience, and/ or a low tolerance for risk. Never execute a trade unless you can afford to and are prepared to lose your entire investment. In addition, certain trades may result in a loss greater than your entire investment. Always perform your own due diligence and, as appropriate, make informed decisions with the help of a licensed financial professional.
Commissions, fees and other costs associated with investing or trading may vary from broker to broker. All investors and traders are advised to speak with their stock broker or investment adviser about these costs. Be aware that certain trades that may be profitable for some may not be profitable for others, after taking into account these costs. In certain markets, investors and traders may not always be able to buy or sell a position at the price discussed, and consequently not be able to take advantage of certain trades discussed herein.
Be sure to read the OCCs Characteristics and Risks of Standardized Options to learn more about options trading.
Related Posts